The soil penetration resistance, $PR$, is an important soil characteristic that can affect plant root growth. However, $PR$ is not static, and it depends mainly on the soil moisture, $s$ (or $\theta_v$ if it is represented as volumetric soil water content), and bulk density, $\rho_b$. Considering that bulk density is constant over the growing season, the fluctuations in PR will be related to soil moisture, which depends on the rainfall in rainfed systems. Although there are several equations to represent the relationship between $PR$ and soil moisture, this relation can be described as:

\[PR(\theta_v, \rho_b) = \exp(a + b \cdot \rho_b + c \cdot \theta_v)\]

Thus, $PR$ is low when soil moisture is high, and it increases exponentially as soil moisture decreases.

The soil moisture can be modeled using a stochastic model:

\[n Z_r \frac{ds}{dt} = R - C_I(R) - Q(R,s) - L(s) - ET(s)\]

where $n$ is the soil porosity, $Z_r$ is the effective root depth, $s$ is the relative soil water content at time t ($s_h < s \leq 1$), $R$ is the rain, $C_I$ is the canopy interception, $Q$ is the runoff, $L$ is the leakage, and $ET$ is the evapotranspiration. Details of the model and parameterization are described by Souza et al. (2021).

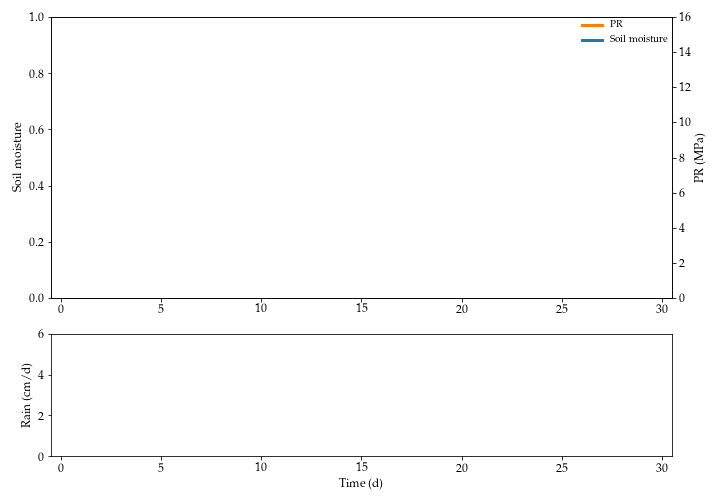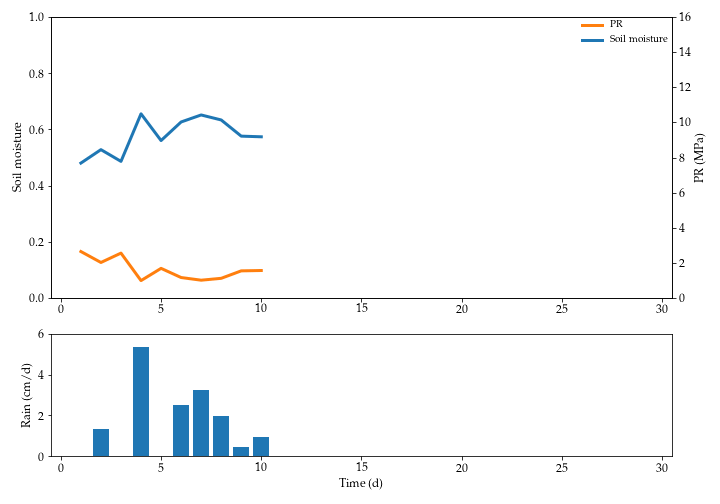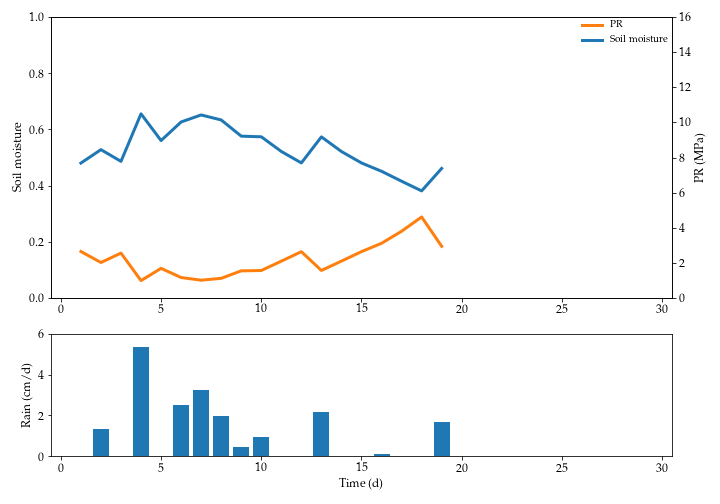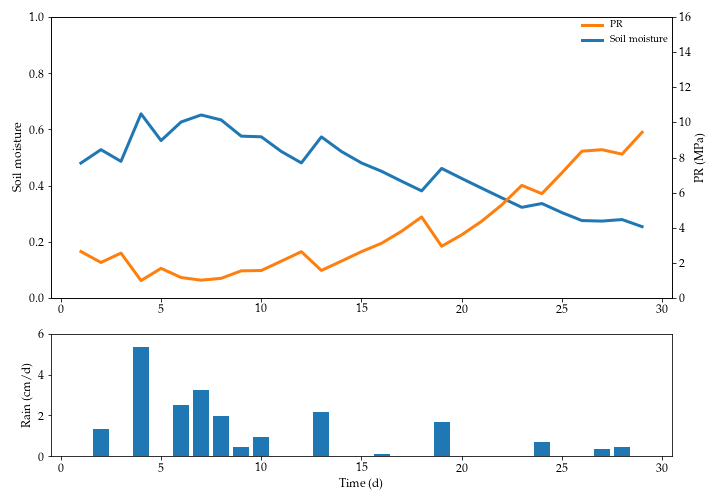
An example of the soil moisture and $PR$ dynamics is shown below.